目录
模拟与动画
简介
动画是一种信息传递的工具。
常用帧率:
- 电影:24FPS
- 视频:30FPS、29.994FPS
- VR:90FPS+(不晕的基本要求)
- 游戏:30、60FPS+
动画里程碑
- 3200BC-远古时期人类的壁画-Shahr-e Sukhteh, 伊朗
- 1931-Phenakistoscope圆盘,通过转动圆盘来做动画
- 1878-第一部电影Sallie Gardner
- 1937-第一部剧场版手绘电影-白雪公主与七个小矮人
- 1963-第一个计算机生成的动画
- 1972-早期计算机动画,人脸动画
- 1993-侏罗纪公园
- 1995-玩具总动员,第一部完全计算机生成的动画电影(光栅化)
- 2009-天降美食
- 2019-冰雪奇缘2
关键帧动画
- 最早是由最厉害的原画画出关键帧,其他助手画出之间的差值(渐变帧)
- 现在通过插值补充两个动画中的差值
- 线性插值一般过渡不那么自然
- 使用b样条之类的平滑插值技术
物理模拟
介绍
- 通过建立真实的物理模型来模拟出真实的动画系统
- 例子:布料模拟、流体模拟
质点弹簧系统
简单定义:一系列相互连接的质点和弹簧
- 理想弹簧:
- 胡克定律:fa-b=-k·(b-a),k:劲度系数
- 牛顿第三定律:fb-a=-fa-b
- 问题:没有初始长度
- 非零长弹簧:
- 引入原长l||b-a||
- ||b-a||-l 为弹簧被拉伸的长度
- b-a/||b-a||表示a->b力的方向,是归一化
- 问题:由于没有阻力会永远震荡
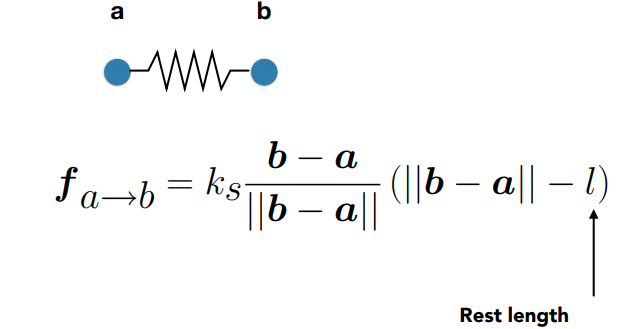
- 加入阻尼力:
- 再讲内容之前先普及一点:x为位移,x上一点是速度(一阶导数)点两个点是加速度(二阶导数)
- f是阻尼力,b加上一点是速度,kd是劲度系数
- 问题:无法描述弹簧内部的力
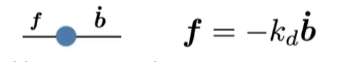
- 完善的阻尼力:
- 红框为b与a相对速度在b与a方向上的投影,是一个标量
- 红框右边是a到b的方向

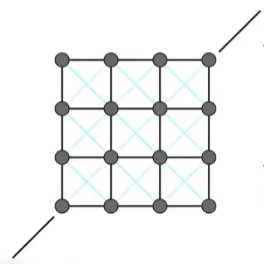
问题:这样的弹簧系统无法应对对折的情况(比如讲一块布对折)
解决:通过加入斜向的弹簧来解决这样的问题。
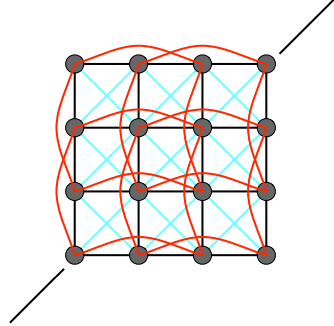
问题:这样的弹簧系统无法应对沿着弹簧竖着对折的情况
解决:加入跳跃连接的点,隔一个支点加一个弹簧,这个弹簧十分的弱
有限元法FEM
- 方便制作力的传导
- 应用于车辆碰撞的模拟
粒子系统
粒子生成步骤
- 生成粒子
- 计算每个粒子的力(难点)
- 更新每个粒子的位置速度
- 将死亡的粒子移除
- 渲染
粒子之间的作用力
- 引力与斥力
- 重力
- 电磁力
- 阻尼力
- 摩擦
- 空气阻力
- 粘度
- 碰撞
- 墙壁
- 容器
- 物体
应用
通过制定规则让粒子表现群体的个体之间的关系
- 鸟群
- 每个个体的鸟不愿意落单
- 同时不愿意离群体太近
- 方向相对统一
- 细胞结构
- ...
单个粒子的模拟
获取单个粒子的速度场,获取场内任意位置的速度参数
计算速度场内粒子的位置需要计算一阶常微分方程
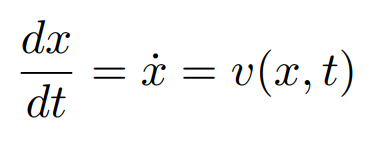
欧拉方法
对时间做离散化的操作,利用欧拉方法(前向欧拉)获取每一个时刻的速度和位移
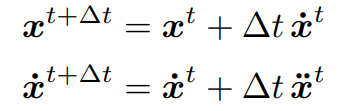
问题:误差大、稳定性不足,如果步长不足则会不准确,且对于一些曲线的模拟十分不准确,一定会正反馈,其中不稳定的问题很致命
解决:
- 中点法
- 自适应改变步长的方法
- 隐式法
- 不基于物理的方法:基于位置法、韦尔莱积分
中点法
- 在初始点使用欧拉方法计算出下一位置的a点
- 在初始点与a点总取中点b
- 再使用b点的速度来求出初始点下一位置c点

中点法完整公式:
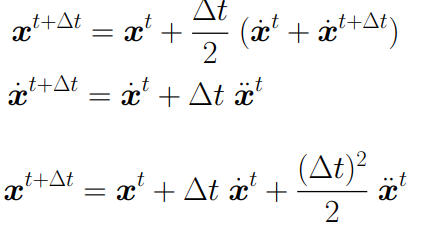
自适应步长
计算两遍,一次是Δt,一次是Δt/2来进行欧拉方法
若两遍的结果相差较大,则应将步长减半重新计算
隐式欧拉方法
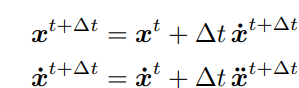
联立方程组解出结果(假设下一个时刻的加速度已知)
龙格库塔法
是一种四阶的方法,稳定性相对来说比较好。
中点集合k、k2、k3、k4通过下面的方法进行计算得到下一时刻的位置。

不基于物理的方法
- 比如基于位置法、韦尔莱积分等方法
- 该方法不保证能量守恒
- 只通过调整某些位置,使其能够满足模型中的一些特定性质。
- 是一种不稳定的方法,但是简单且实现时间快。
如何判断方法是否稳定?
- 通过研究局部截断误差O(h2)和总体累积误差O(h)来确定稳定性
- 当在局部上讲Δt变为1/2Δt时,在全局上Δt会变为1/4Δt
- 因此阶数越高越好,减少阶数,误差可以成倍的减小
运动学
分为正向和反向,模拟的是真实的骨骼运动
正向运动学
关节类型:
- 可以绕着关节2维的旋转
- 可以绕着关节3维的旋转
- 可以拉长一部分的关节
我们可以通过参数很容易计算出p点的坐标,通过改变参数来实现骨骼的动画就被称为正向运动学
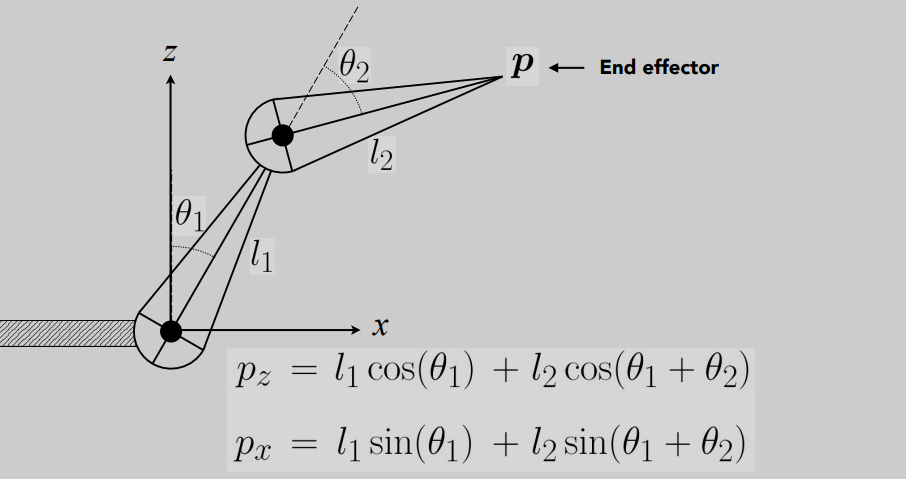
因为这样的操作十分不直观,艺术家们不愿意通过这样的方式来调节模型的骨骼,因此逆运动学应运而生
逆向运动学
通过直观的控制尖端p点来直接控制参数,这样操作的计算量相对正运动学相比明显增大
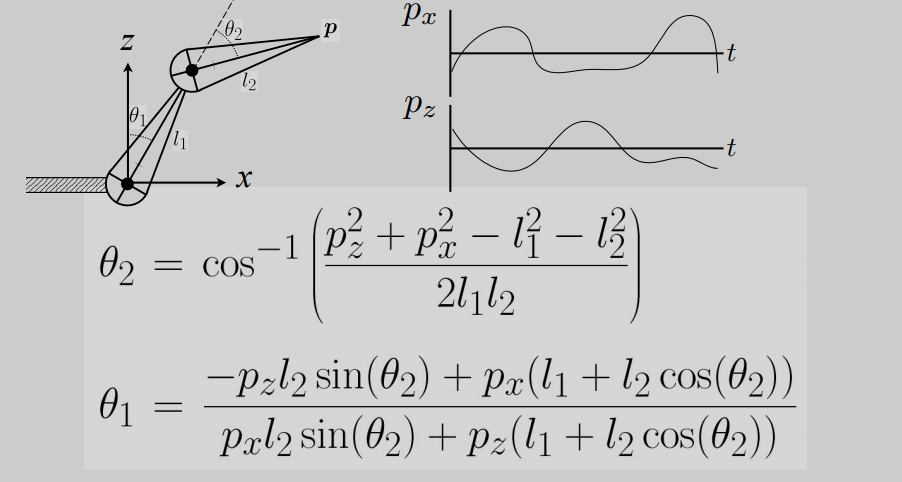
问题:
- 解并不唯一:有多个可能性造成p点在所在坐标
- 无解:p点不可能在指定的坐标
解决:我们通过随机化算法(优化方法、梯度下降)等方法来解决问题,并不使用纯数学的方法来暴力解决
例子:Style-Based IK
骨骼绑定
在模型上增加控制点,让人们能够方便的调整模型的动作
对于同一个模型的两个动作,通过控制点间的位置插值计算来完成,这被称为“Blend Shapes”
动作捕捉
在真人身上放置控制点
优点:
- 可以快速捕捉大量数据
- 较为真实
缺点:
- 复杂、昂贵
- 动作常常会不满足要去,需要后期调整
- 捕捉条件限制
捕捉方法:
- 光学
- 磁力
- 机械
动画的制作流程:
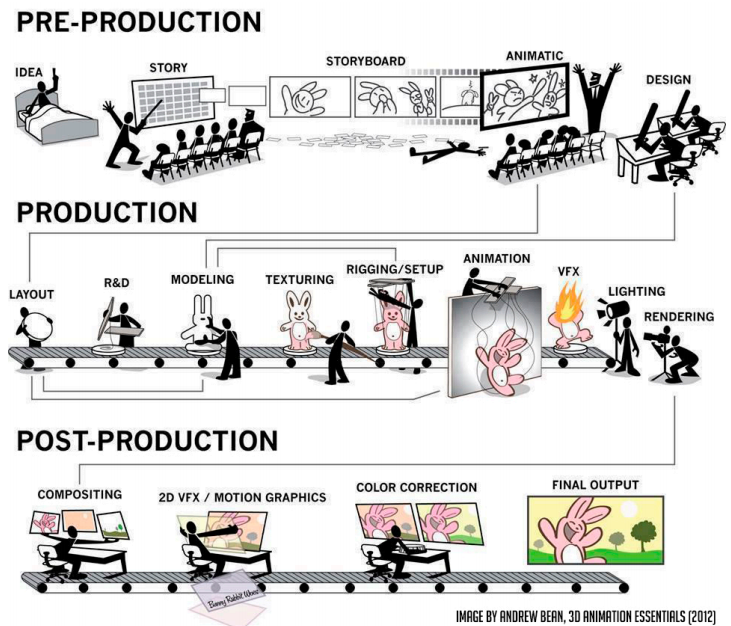
刚体模拟
刚体不会发生形变,通过求得下面的参数通过上面粒子模拟的方法计算出任意时刻的位置
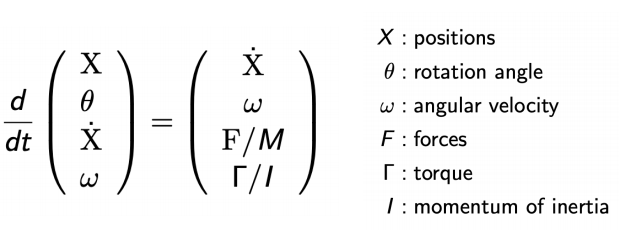
流体模拟
定义
- 水体是由多个刚体小球形成的,不可压缩
- 模拟与渲染是分开的过程
实现思路
- 通过获取任意时刻小球的分布位置来获取小球单位面积的密度
- 如果密度如果发生改变(不同于平静的水面),就通过通过改变小球的位置来修正位置,让水总有一个趋于平静的趋势
- 通过加入能量损失让水最终停下来
质点法和网格法
质点法和网格法流体模拟中的两个不同的思路
质点法(拉格朗日法):逐个模拟每个粒子
网格法(欧拉方法):将一个空间定义为一个网格,通过观察以网格为单位的时间如何变换来模拟
混合方法MPM
- 质点:将不同的粒子的不同属性储存在粒子上
- 网格:模拟变换的过程在网格中完成
- 将每一个时刻网格的信息写回网格内的粒子上
参考资料
完整笔记
- 度盘链接
- 提取码:njcf











 加油
加油


