目录

1.导论与数学基础

2.变换

3.光栅化

4.着色

5.几何

6.光线追踪

7.材质与外观

8.高级图形渲染概要

9.造型机、镜头和光场

10.颜色与感知

11.模拟与动画

导论

图形学应用场景

  • 电子游戏：
    • PBR：之狼
    • 卡通渲染：无主之地
  • 电影： 黑客帝国
  • 动画： 疯狂动物城、冰雪奇缘
  • 设计： 概念图
  • 可视化： 虚拟现实
  • 数码插画： 模拟仿真
  • GUI图形用户接口
  • 字体设计： 矢量图

全局光照做的好不好影响游戏美术品质，同时体现在场景的亮度

图形学的技术挑战

光栅化(rasterization)：

将三维空间中的几何形体显示在屏幕上

实时：30fps 否则被成为离线

曲线和网格(Curves and Meshes) ：各种细分方法

光纤追踪(ray tracing)：动画电影广泛使用，但是速度较慢

目前使用游戏使用的是实时光线追踪

仿真和模拟（animation/simutatoin）

OpenGL、dx是图形学API不是图形学

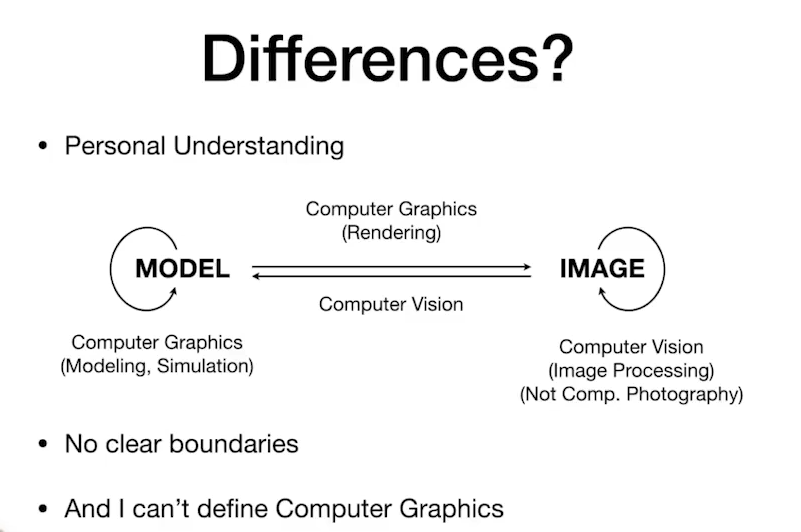
计算机图形学与计算机视觉

  • 图形学不是计算机视觉。
  • 计算机视觉：猜测、预测、分析处理
  • 计算机视觉是理解这个世界，计算机图形学是创造这个世界
1

线性代数复习

图形学默认使用列向量，课程默认为右手系

点乘在图形学的应用

AB=|A||B|cosθ

  • 点乘主要应用于求两个单位向量的夹角，
  • 观察两个向量之间是同向、垂直还是反向，可以观察两个向量的接近，若两个向量的点乘接近1则离得很近，若接近0则离得很远
  • 利用投影可将一个向量分解成两个（多个）向量和

叉乘在图形学的应用

  • AxB=-BxA
  • 判定左右（内外）
    • 二维：若AxB为正则点B在点A的左侧，AxB为负则B在A的右侧
    • 三维：若点P在点A、B、C内，则ABxAP，BCxBP，CAxCP结果都为正（负），若任意一个结果不同则P在ABC外，如果结果都为0，则可以认为P在A、B、C内也可以认为P在A、B、C外
  • 定义坐标系
    • 要求：单位向量、互相垂直（点乘为0且叉乘结果为另外一轴）
    • 可以获得任意一个向量分解为多个投影

矩阵知识点

  • （MxN）（NxP）=（MxP）
  • 矩阵没有交换律，只有结合律
  • 转置：(AB)T=BT AT
  • 单位矩阵I（对角阵I）：可以算出矩阵A-1(A逆)，可以用于返回变换前的结果
  • 向量的点乘、叉乘都可以转换为矩阵相乘
  • 点乘：AB=ATB
  • 叉乘：AxB=A*B

概率论复习（用于路径追踪）

X：随机变量

pi一定是非负的，所有pi相加等于1

EX:数学期望

X~P(X)：概率密度函数，概率的连续分布情况

概率论1

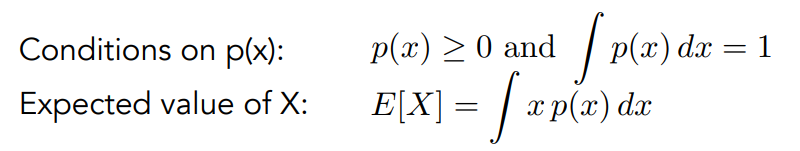
参考资料

GAMES101-现代计算机图形学入门-闫令琪

完整笔记

赏