目录
变换
2D 变换
缩放
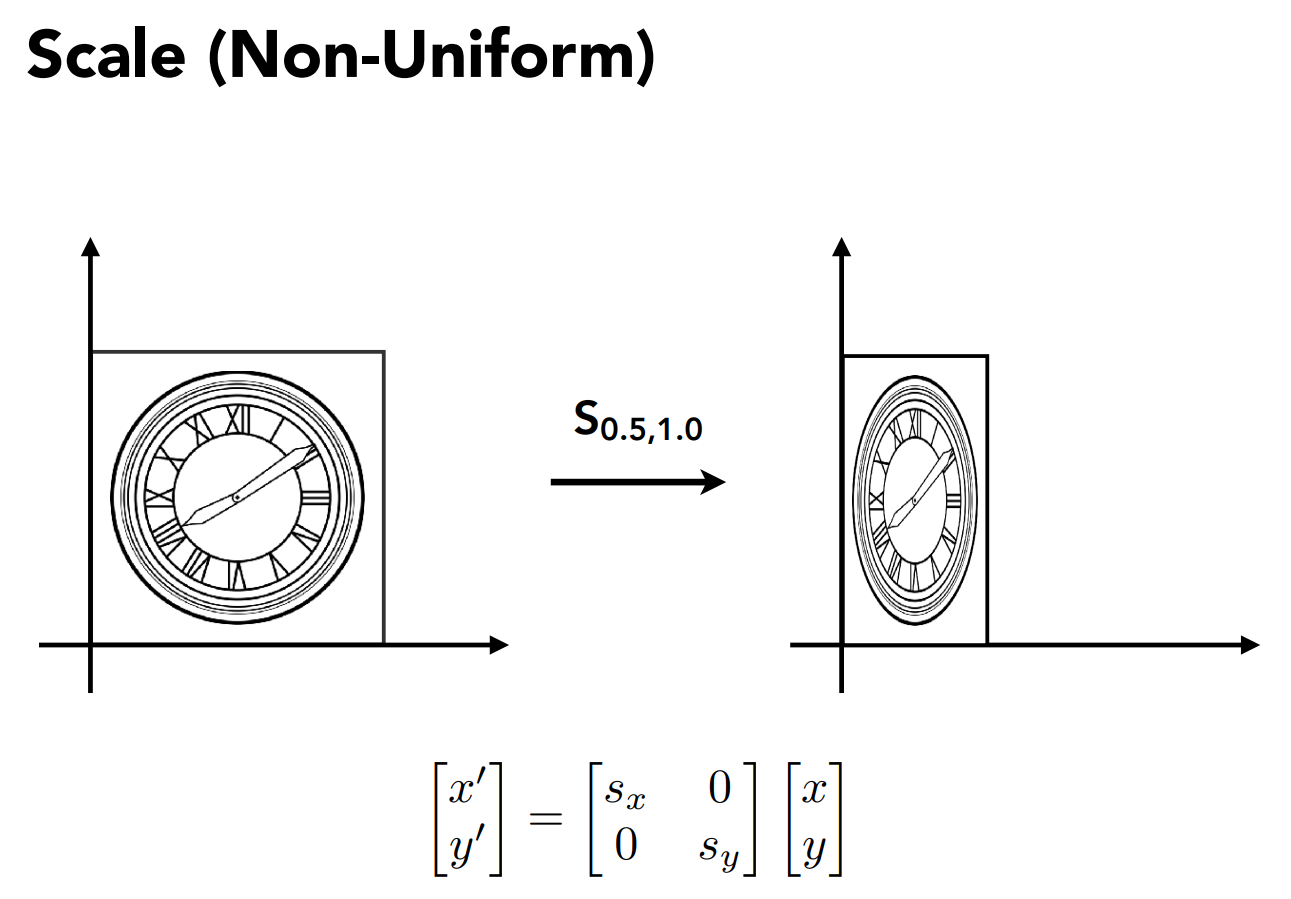
- X'=SX
- Y=SY
X轴翻转
- X'=-X
- Y'=Y
切变
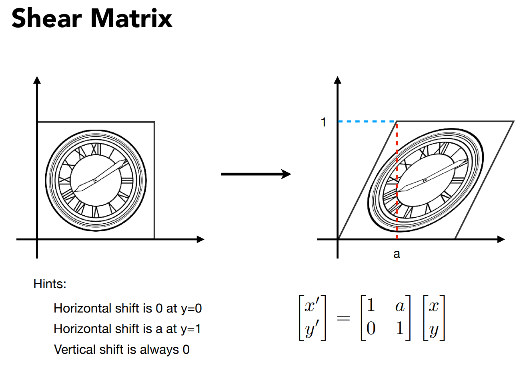
旋转
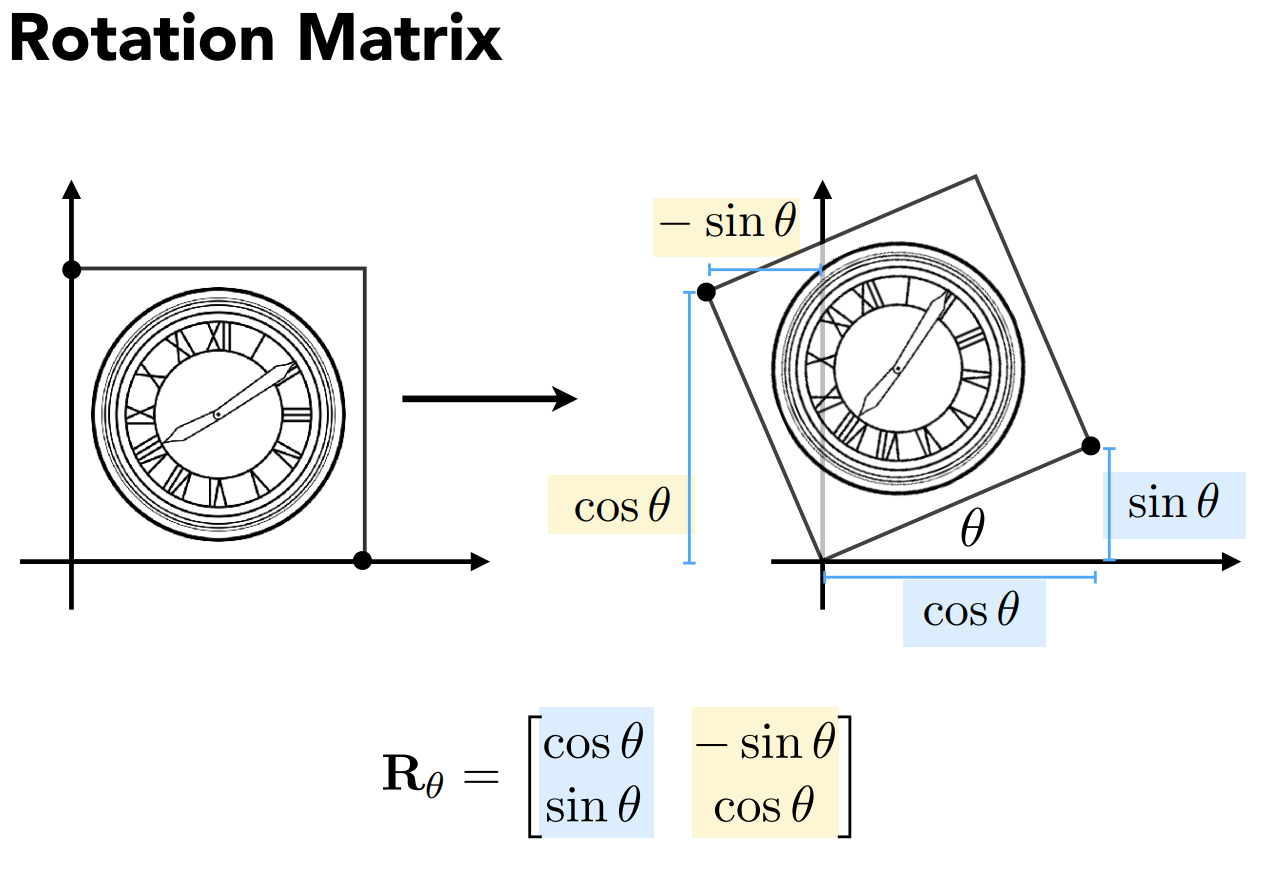
R-θ=RθT
齐次坐标

为了解决平移产生必须要用加法的问题,加入齐次坐标。
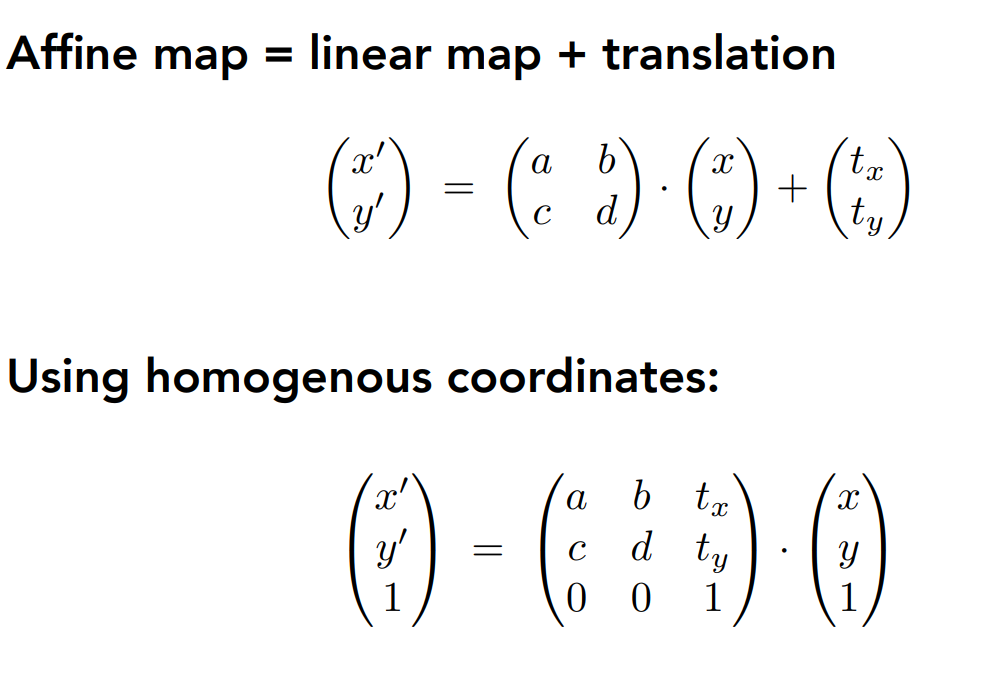

- 矩阵没有交换律:同时需要平移和线性变换的时候,需要先线性变换再平移
- 仿射变换=线性变换+平移
3D 变换
齐次坐标
3D点:(x,y,z,1)T
3D向量:(x,y,z,0)T
旋转向量与欧拉角
RXYZ(α,β,γ)=RX(α)Ry(β)Rz(γ)
利用右手螺旋定则
在三维坐标系中:
XxY=Z XxZ=-Y YxZ=X
因此RY(α)中为X或Y的转置

同时,去掉分别代表XYZ运算的行列即可变换为最基本的旋转式
罗德里格旋转公式
这是一种可以表示任意旋转后的向量
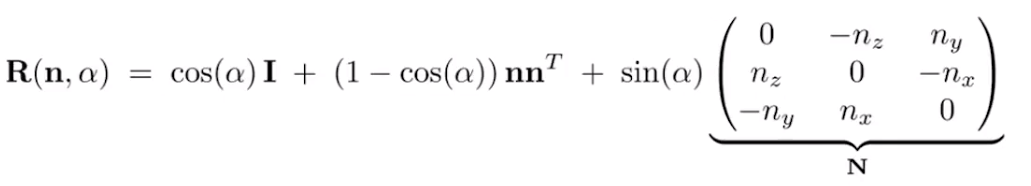
四元数解决了两个旋转角度中差值的问题,本课中不具体讲解
视图变换
什么是视图变换?
视图想想如何拍一张照片:
- 找一个好的地方并安排好拍照的人(模型变换)
- 找一个好角度并放好相机(视图变化)
- 茄子!(投影变换)
定义相机
-
position(相机在哪)e
-
look-at/gaze direction(朝哪个方向)g
-
up direction(向上方向:控制歪斜)t
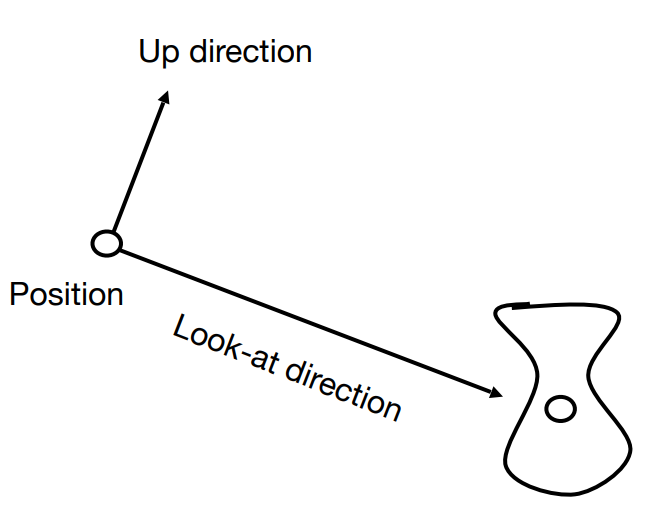
同时,相机默认的向上方向为+Y。永远朝着-Z方向看,永远在原点上。
把任意点相机移到默认点
-
先平移
-
再旋转(利用逆矩阵的性质,先算从原点到任意点再转置过来)

(g x t = e)
投影变换
正交投影:更像工程制图,没有近大远小的性质
透视投影:近大远小,更类似于现实中的形态
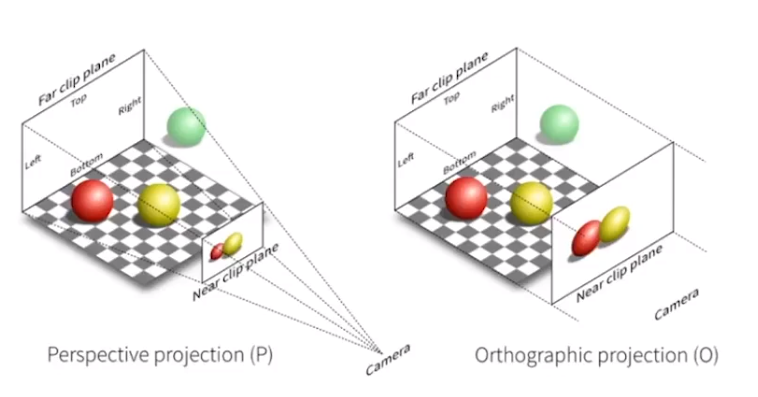
正交投影
一种简单的理解方式
- 把z轴去掉
- 相机位于原点,看向-Z轴,向上为Y轴
- 将生成的矩形平移并缩放为[-1,1]²
标准方式
总的来说,要将任意的立方体变成标准(canonical)立方体
先做平移,再做缩放
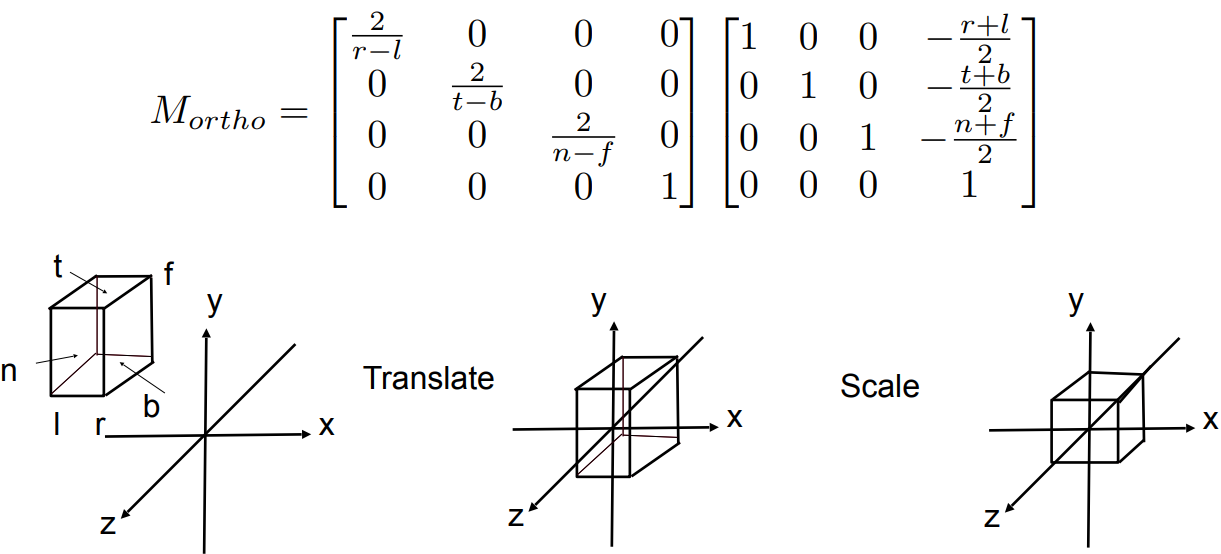
透视投影
如何做透视投影?
- 将视锥体压扁成立方体
- 做正交变换
“压扁”操作
其中:
n为近平面
f为远平面
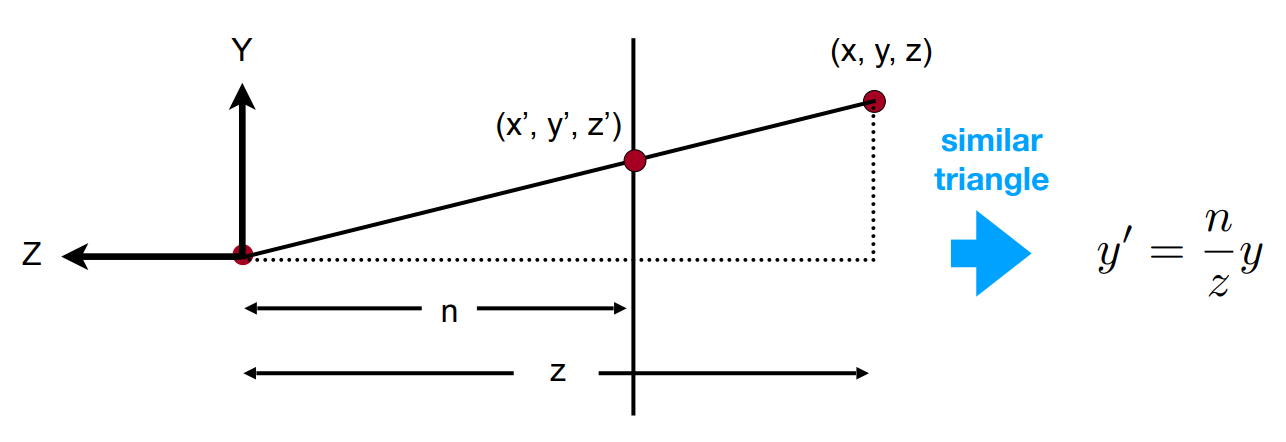
利用相似三角形求出y轴的位置
同理可以得到x'=(n/z)x
Z轴如何处理?
当我们完成X、Y轴处理后,发现Z轴仍不知道,同时乘z后得到右下的矩阵
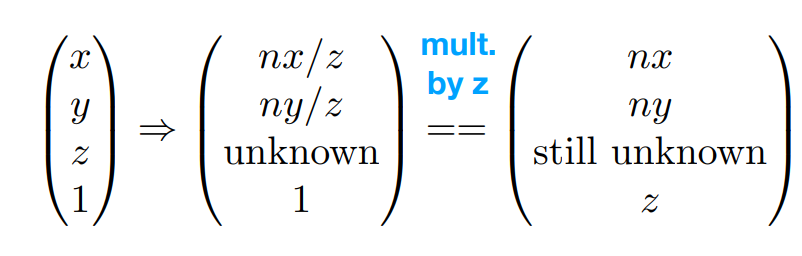
同时可以通过矩阵叉乘得到未知矩阵的一部分:
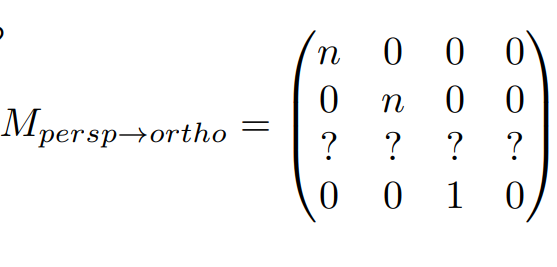
(?,?,?,?))->(0,0,?,?)
再通过下图的方法得出原本"still unknown"的数值为n²

以此得到:
An+B=n²
同时z轴在远平面上的数值并不会改变,因此得到:
Af+B=f²
通过解上面两个方程得到:
A=n+f
B=-nf
因此Z轴一行的矩阵为:
(0,0,n+f,-nf)
参考资料
完整笔记
- 度盘链接
- 提取码:njcf











 加油
加油






