目录

1.导论与数学基础

2.变换

3.光栅化

4.着色

5.几何

6.光线追踪

7.材质与外观

8.高级图形渲染概要

9.造型机、镜头和光场

10.颜色与感知

11.模拟与动画

几何

几何表示方法的分类

• 隐式
  • 可以通过一个函数来表示的几何体。
  • 例如圆可以表示为f（x，y，z）=0
  • 优点：可以很容易判断某个点是否在几何体上
  • 缺点：难以通过函数判断出几何体的真实形状
• 显式
  • 通过参数映射表示的几何体（uv坐标转换为xyz坐标）
    • 参数映射：通过某个带有u，v的函数分别表示出x，yz的坐标
  • 直接给出几何体
  • 缺点：难以表示出某个点是否在几何体上。
  • 优点：容易看出来几何体的真实形状

隐式表示

对于复杂的几何体十分不友好。

隐式几何

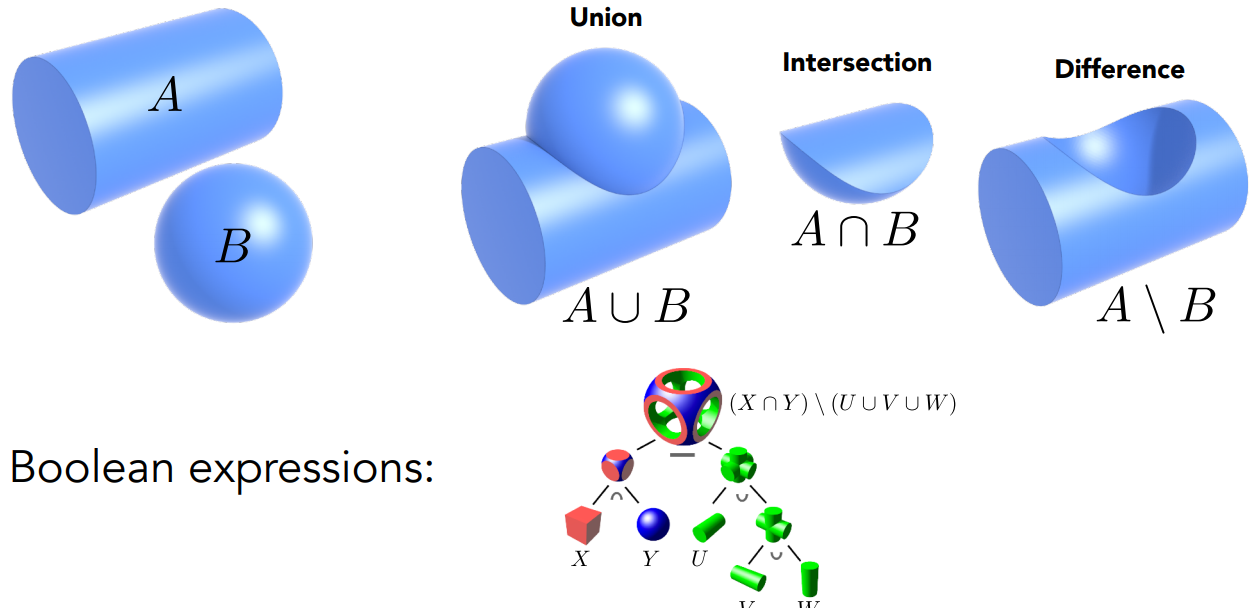
CSG(Constructive Solid Geometry)

复杂的几何体通过简单几何体进行集合运算（交并补）得到，该操作被称之为CSG。

距离函数

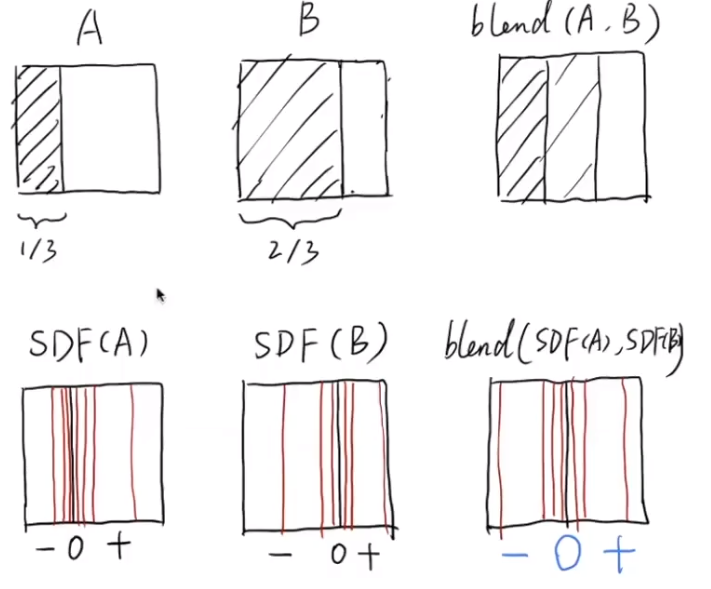
下图A与B相进行融合操作后得到blend（A,B)，左边三分之一完全被挡住，中间被挡住一半，最后边完全没被挡住。

距离函数：任何一个点到达边界的最短距离。

通过AB距离函数相加得到融合后的SDF图，可以转化为blend（A,B)这张图。

距离函数可以将两个靠近的集合体进行融合。

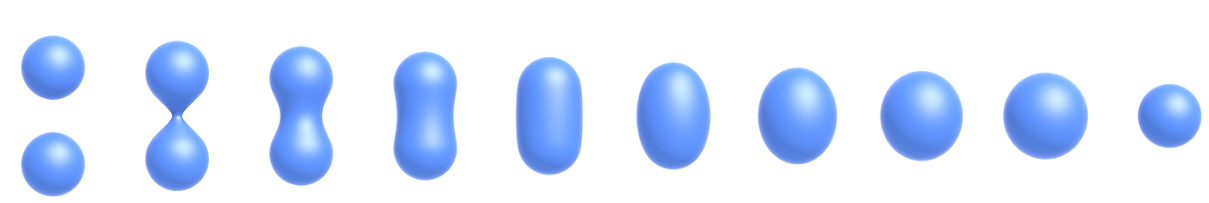
距离函数通过水平集（LevelSet）得到F(X)=0（边界）

分型

分型这种递归问题在渲染中会引发严重的走样

显式几何

点云

• 用密集的点放在空间中
• 是某个坐标系下的数据集
• 每个点包含了坐标、颜色等一系列信息
• 只要采样足够密集，理论上可以表示任意集合体
• 如果采样不够密集，将会无法分辨模型的形状
• 应用：激光扫描

多边形网格

简介

• 讲面拆解为多边形（大多是三角形和四边形），存储顶点和多边形信息
• 在图形学中应用的最为广泛

如何储存多边形信息？

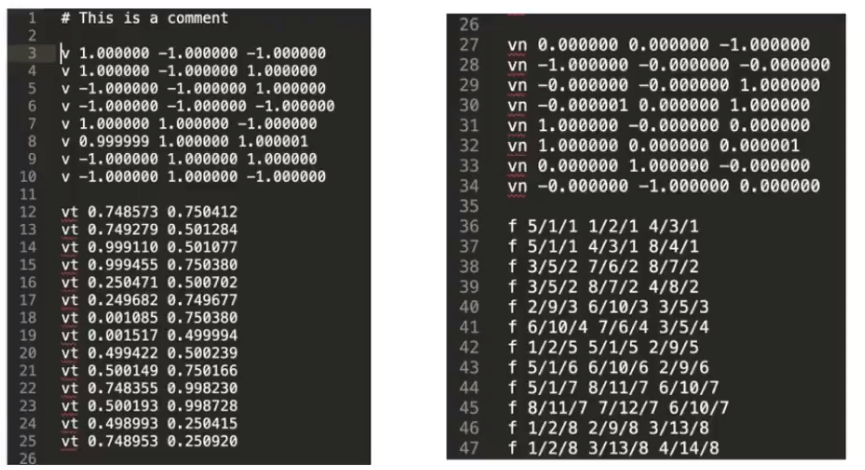
使用OBJ格式讲几何体的点、法线、纹理坐标分别表示，然后再表示，面与面的连接关系。

下图定义了一个立方体，有八个顶点（V）,六个面（Vn）多个纹理坐标（vt）表示，然后使用f表示他们之间的关系（（f V/Vt/Vn）

贝塞尔曲线

只要求一定要经过起止点，起止点之间的若干个控制点用于控制曲线弯曲的方向，最终形成一条经过起止点的光滑曲线被成为贝塞尔曲线。

德卡斯特里奥算法

通过德卡斯特里奥算法法来绘制贝塞尔曲线。

• 引入参数t（范围 为0-1）
• 取b0到b1，b1到b2上t位置的点b0‘，b1’
• 将b0‘，b1’连接
• 取b0‘到b1’t位置上的带你b0‘’
• 将所有的0-1所有的b0‘’点都遍历一份相连即可得到贝塞尔曲线
• 若有n个控制点则将上面步骤进行递归操作直到找到最终位移b0ⁿ

总结得到公式：bⁿ(t)=b0ⁿ(t)=Σb0Bⁿ(t)

可以求得一个以t为自变量的函数，由这些点形成的集合构成贝塞尔曲线

其中：

• b为n个贝塞尔控制点
• Bⁿ为伯恩斯坦多项式

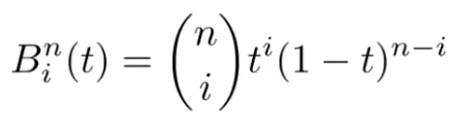
其中：

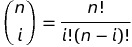
（排列组合Cni）

例子：b0、b1、b2、b3为3d空间中的点，通过函数求得n个离散的点

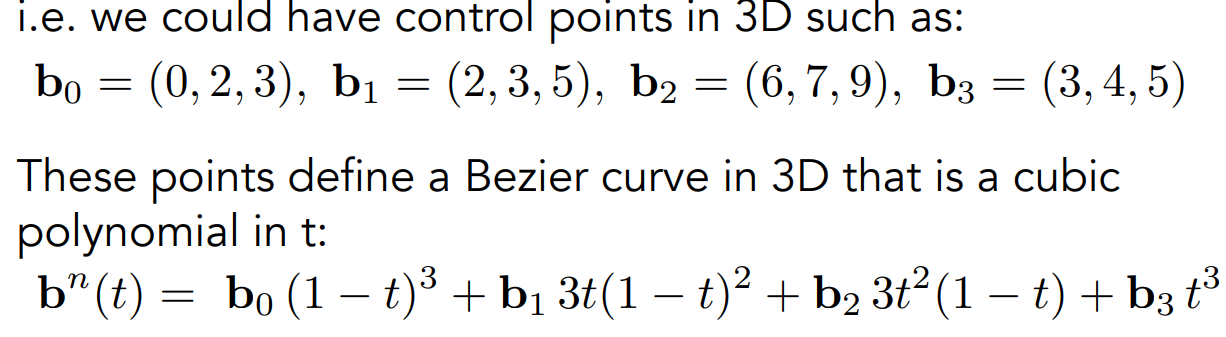
• 对贝塞尔曲线做仿射变换只需要对控制点、起止点做仿射变换再重新绘制一遍即可。
• 对投影变换没有这样的性质

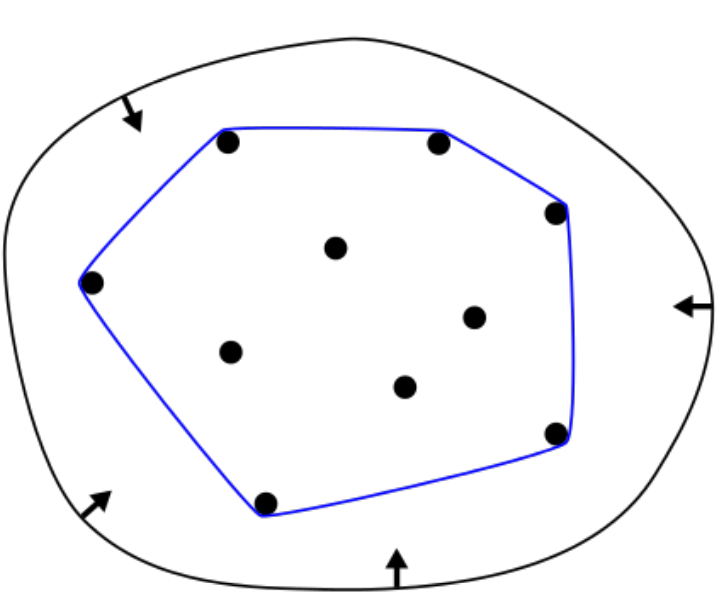
凸包

贝塞尔曲线拥有凸包的性质。

连接贝塞尔曲线最外围的控制点，将其相互连接形成一个封闭空间，画出来的贝塞尔曲线一定在凸包范围内。

若贝塞尔曲线是一个直线则凸包也是一个直线。

逐段贝塞尔曲线

当控制点太多会影响控制点的效果。

每四个控制点定义一条贝塞尔曲线，然后再将他们连接起来。

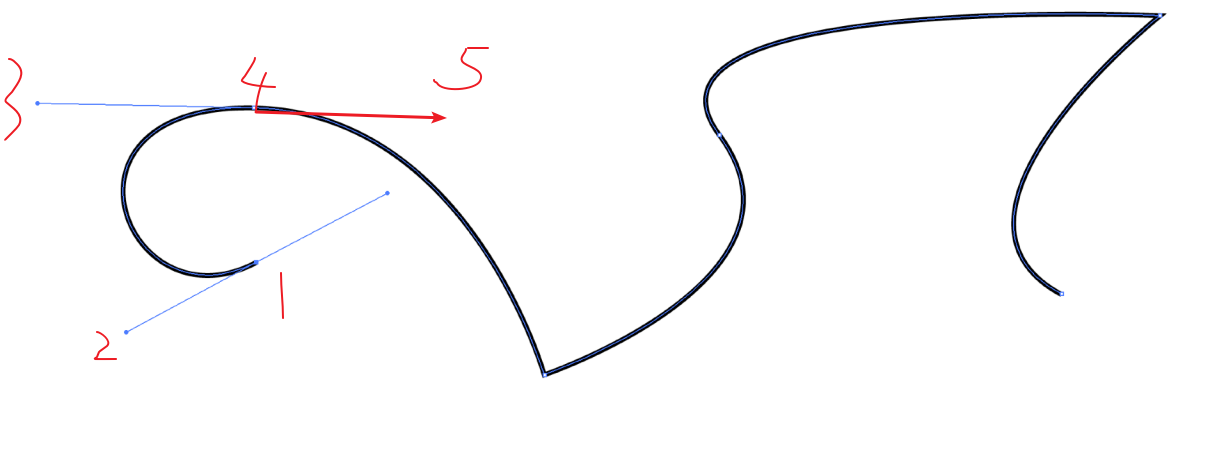
类似PhotoShop的钢笔工具

若想要逐段贝塞尔曲线平滑过渡则需要将相邻控制点共线（如3，5）否则会出现该曲线后边段的不平滑现象。

CN连续

将两个逐段贝塞尔曲线中的两部分连接，连接点被称之为C0连续

若相邻两个控制点距离连接点相同且共线则该连接点被称之为C1连续（再连接处一阶连续可导）

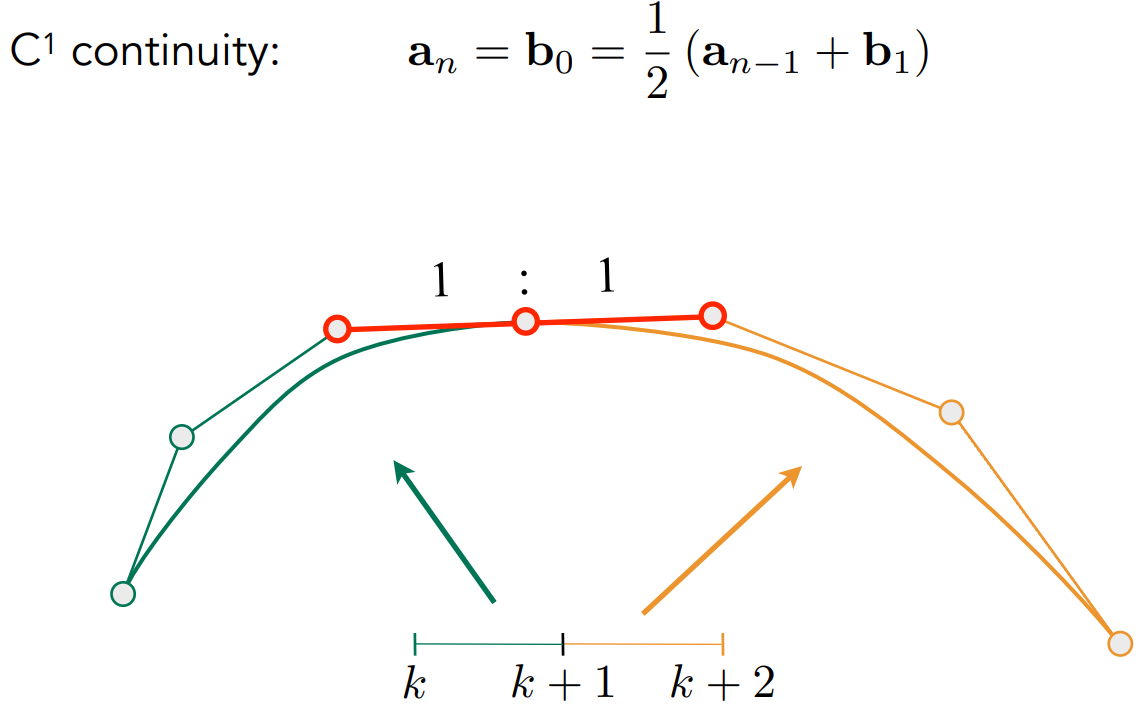
贝塞尔曲面

与二维的贝塞尔曲线思想类似，但是需要定义两个参数u和v（取代之前的参数t）

先对f（u）进行遍历得到曲线，再嵌套遍历得到曲面f（u，v），类似于两层for循环进行遍历

网格操作

网格操作的分类

• 网格细分
  • 让网格的面数更多
  • Loop细分
  • Catmull-Clark细分
• 网格简化
  • 让网格面数更少
  • 边坍缩
    • 通过“二次误差度量”得到坍缩后最优的点
• 网格正规化
  • 让网格中的三角形趋近于正三角形

Loop细分

• 将每个三角形变为4个三角形
• 根据权重指定新的顶点位置
  • 新的顶点和老的顶点以不同的规则来改变自己的位置

对于新的顶点：

V'=3/8 * (A + B) + 1/8 * (C + D)

• V'为新的顶点变换后的位置
• A、B分别为于两个面被共享边的的老顶点
• C、D为非共享边的两个顶点。

对于旧的顶点：

V'=(1 - n*u) * V + original_position * neighbor_position_sum

• V'为旧的顶点变换后的位置
• n为顶点的度（链接的顶点数）
• 如果n=3则u=3/16 其他情况u=3/(8n)
• neighbor_position_sum为邻居点的平均位置
• original_position为旧顶点原本的位置

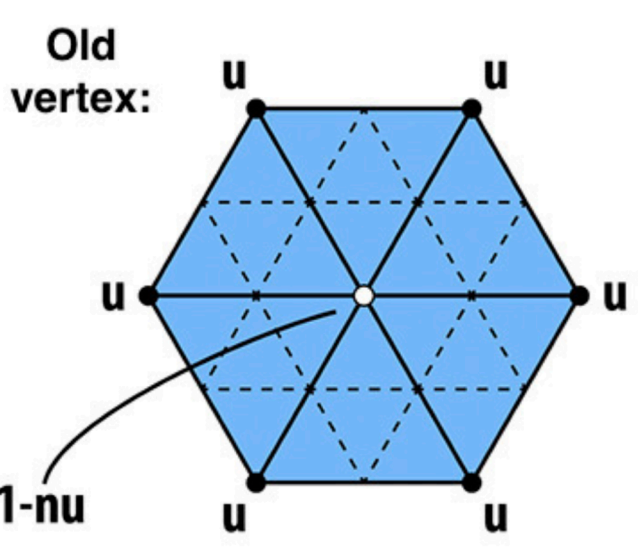
问题：只能对完全为三角形的几何体进行细分

Catmull-Clark细分

相对于Loop细分的优势：可以用于任意不同的面的细分。

奇异点：顶点的度!=4

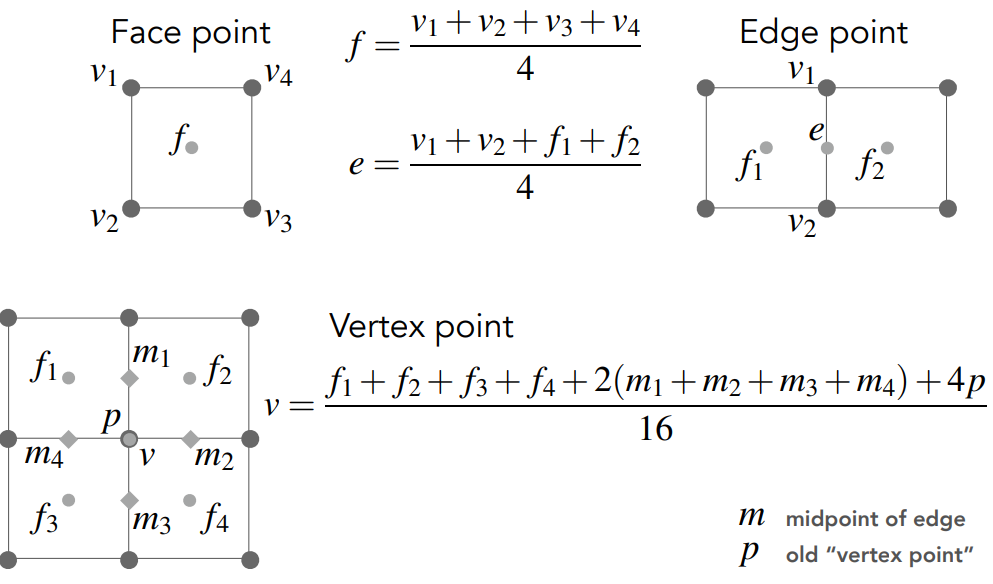
• 将面的中点和面上线的中点连起来
  • 在第一次细分之后，非四边形面数量会加到原本奇异点的数量上
• 面上的中点（f）、边上的中点（e）、老的顶点（v）变化情况如下图

边坍缩算法

通过不断迭代进行边坍缩操作达到简化模型的目的。

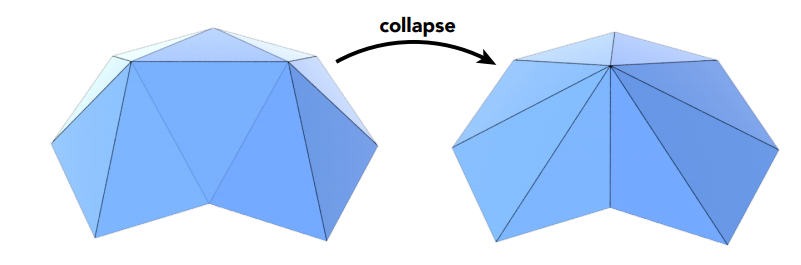
边坍缩面临的问题:

• 坍缩哪些面？
• 如果优先坍缩不重要的面，那如何界定不重要？
• 坍缩后的顶点位置如何描述

二次误差度量

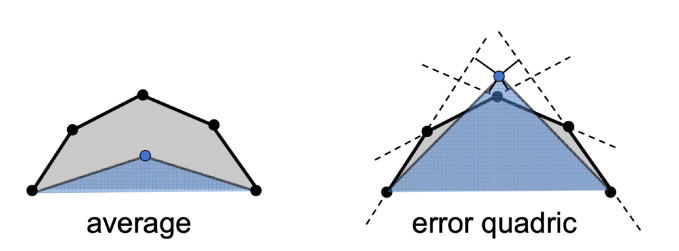
如果将减面时候的点直接平均将会得到左边的图，显然不理想。

通过二次误差度量得到右边的点得到理想效果。

边坍缩算法的步骤

• 对每一条边打一个分数，分数就是他坍缩后的二次误差度量
• 对分数最低（误差最小）的边做边坍缩
  • 用到了Dijkstra最短路径算法
• 重新执行第一步知道完成整个模型的边坍缩

阴影映射（Shadows mapping）

基本流程

• 从光源看向场景并做深度测试
• 从视锥体位置看向场景，从场景中看到的点投影回光源得到该点在深度图中的位置
  • 有些点可以被视锥体看到也可以被光源看到（视锥体投影到的深度图与光源中的深度图相同）
  • 有些点可以被视锥体看到但不能被光源看到（视锥体投影到的深度图与光源中的深度图不符）
• 不能被光源看到的位置但可以被视锥体看到的位置就是阴影的位置

出现的问题

• 只能做硬阴影不能做软阴影（目前以及有技术可以做到）
• 由于shadow map的分辨率问题，阴影可能出现锯齿
• 浮点精度问题，可能在是否能同时被视锥体与光源看到的界定上出现问题引发误差

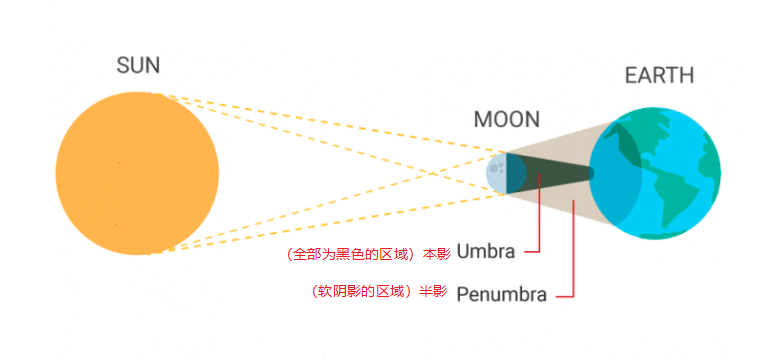
软阴影

软阴影的边缘比较模糊，没有硬阴影锐利的边缘

下图以日食为例子介绍了软阴影在真实物理中形成的原因：

参考资料

GAMES101-现代计算机图形学入门-闫令琪

完整笔记

• 度盘链接
• 提取码：njcf