目录
材质与外观(BRDF)
材质由BRDF决定,或者说材质就是BRDF。
漫反射材质
- 对于一个漫反射材质的物体,我们认为物体本身没有自发光(因此没有Le),且不会吸收光线,照射过来的光线会均匀的反射到四周。
- 且假设入射光是均匀的
- 因此Lo=Li,反射的能量等于收到的能量,因此fr(BRDF)=1/π
- 我们可以引入反射率(albedo)ρ,取值位于0~1让物体能够接受能量获得不同颜色的BRDF
- 下面Lo得出了漫反射材质的渲染方程
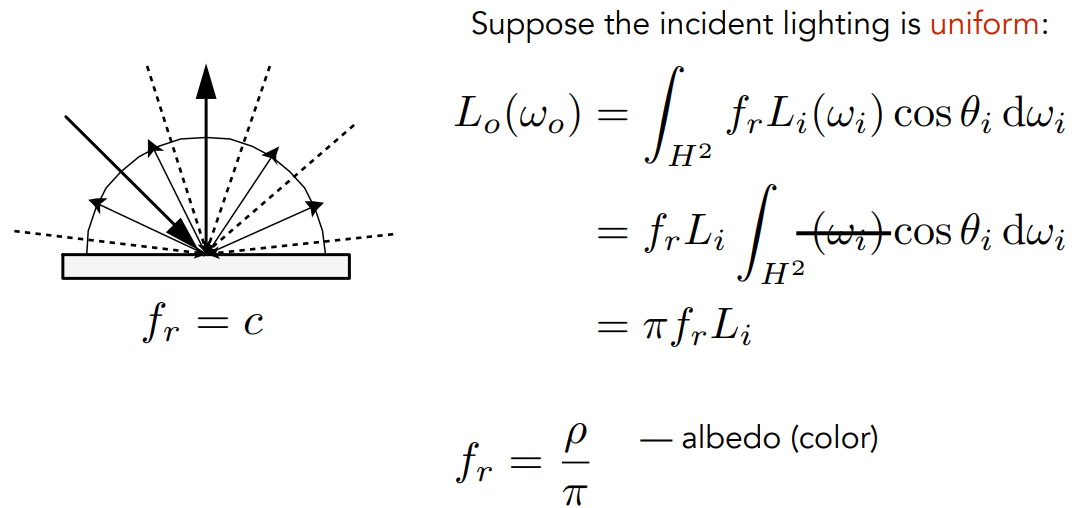
镜面反射
- 在正视图中(左边的图),镜面反射的入射角和出射角可以通过平行四边形法则借助法线方向得出左边的关系
- 在俯视图,又称方位角(右边的图)可以得出右边的关系
- 通过下面的公式可以算出出射角的方向
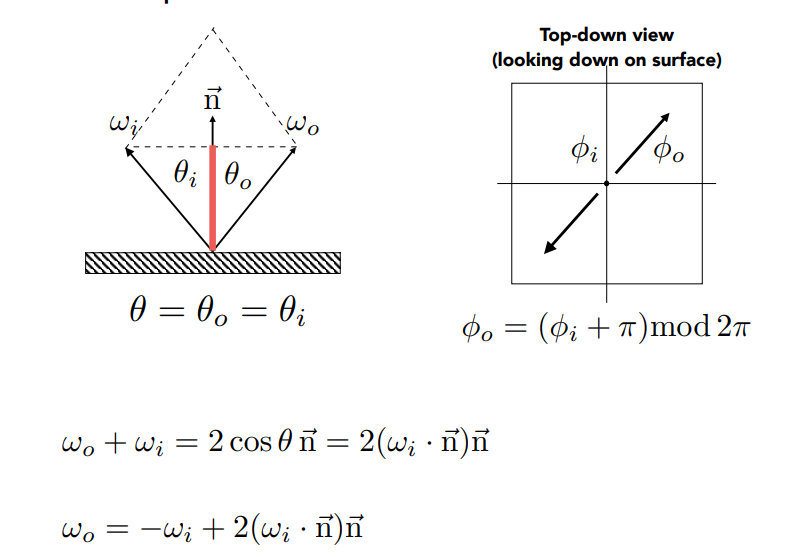
折射定律
斯涅耳定律
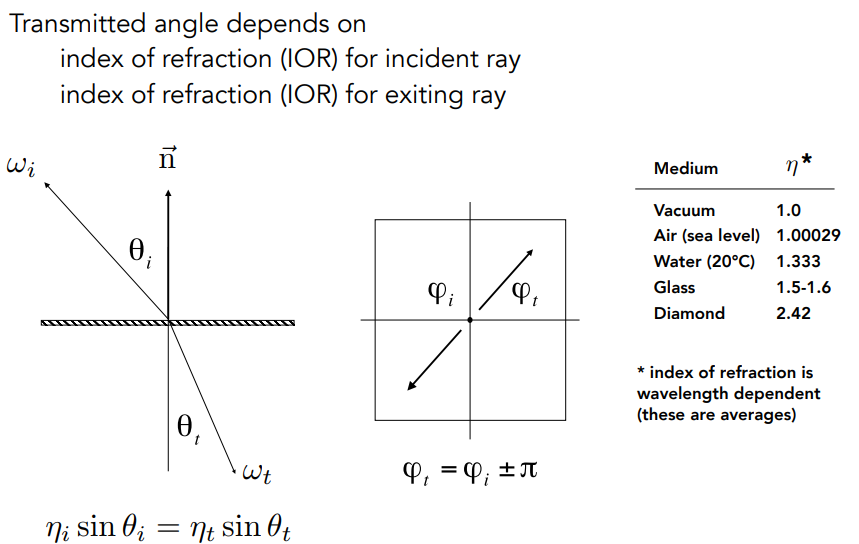
- 引入折射率,右边是常用介质的折射率
- 比如从空气射入水则ηi为1,ηt为1.333
- 通过上面的公式可以计算出出射角的角度
全反射
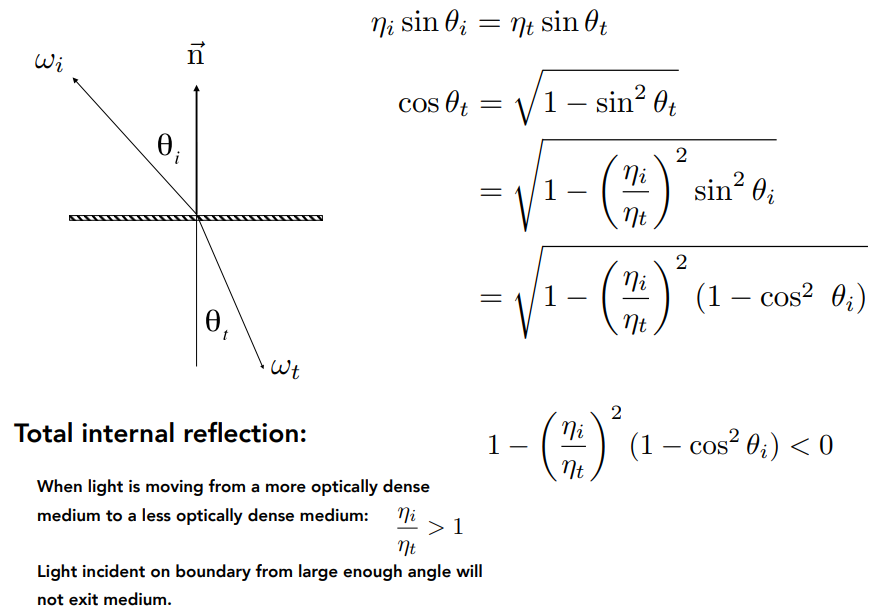
- 当出射角无意义即根号小于0((ηi/ηt)>1)时候,则物体不会发生折射,这种现象被称为全反射
- 例如人在水底往上看,由于发生全反射现象,只能看到一小块锥形的区域,这也被称为斯内尔窗
菲涅尔项
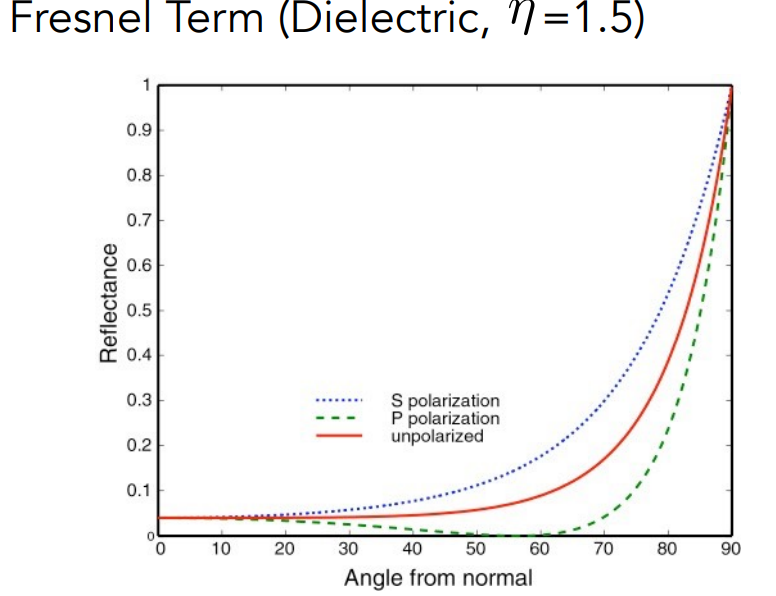
- 当入射角与物体相互垂直的时候,反射会更加明显
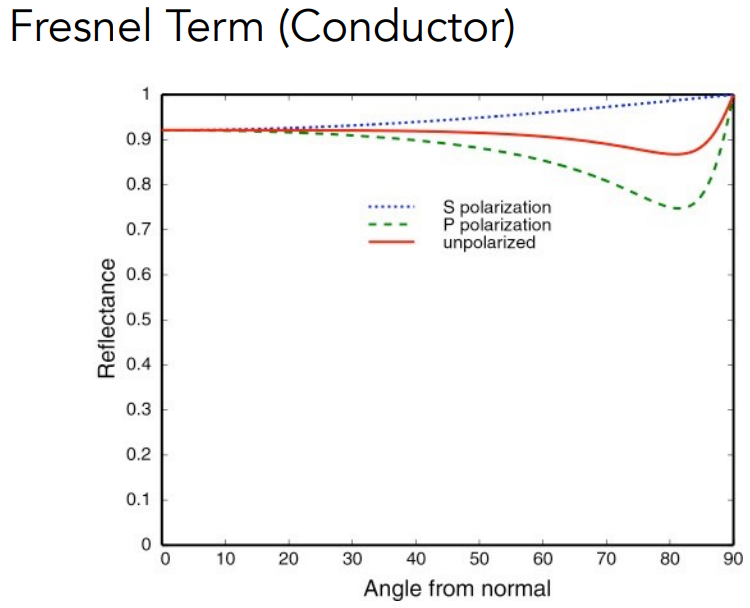
- 菲涅尔项对绝缘体会更加明显(下1图),对导体来说并不明显(下2图)-因为导体的折射率是负数。
菲涅尔项公式:

- 上面的公式是准确的,但是计算十分麻烦,需要考虑极化
- 下面的公式名为 Schlick’s approximation,是一个近似解,图形学中广泛使用。
微表面材质
- 物体表面即使是粗糙的,但是从远处看,我们可以将其看做是一个平的表面
- 例如在空间站中看地球,也可以看到高光反射的地方
- 从远处看是材质,从近处看是几何
- 如果一个表面法线分布集中我们认为他是glossy材质,如果分布分散则认为是漫反射材质
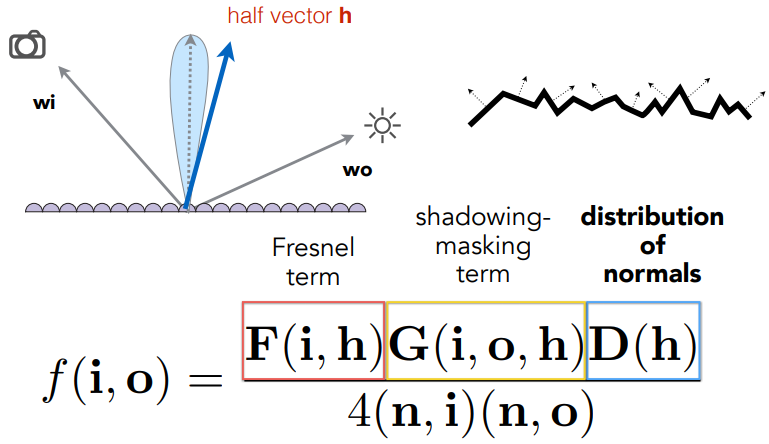
第一个F是菲涅尔项,决定多少能量被反射(垂直时候被反射的能量多,反之少)
第二个G是几何项,计算微表面上的相互遮挡(在grazing angle平着照射微表面的时候容易出现互相遮挡)
第三个D是法线分布,当微表面的法线方向与给定的出入射角的半程向量一定才证明这个微表面的入射方向出射方向正确
各向同性/各向异性材质
 材质的性质进行累加
材质的性质进行累加- 可逆性,对换入射角和出射角可以得到同样的BRDF
- 能量守恒,出射的能量不可能比入射的能量少
- 各向同性和各向异性
BRDF的测量
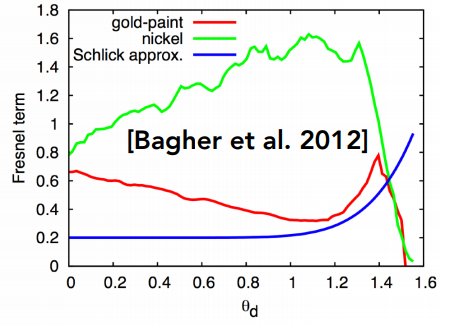
实际测量出来的BRDF和公式推算出来的BRDF经常会有很大差距
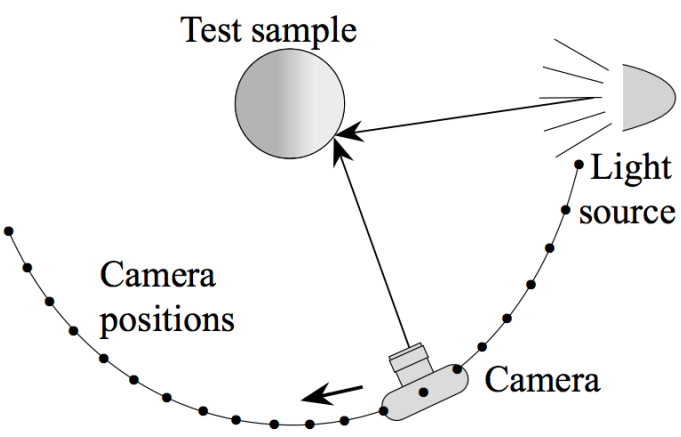
- 可以通过仪器来枚举出测试样例的所有测试点进行BRDF的测量
- 当然这样测量十分的麻烦,我们可以利用BRDF的性质来简化测量
- 比如各向同性的材质只需要测量半圈(由于只有三维且利用可逆性可以只测量半球
- 各种不同的方法来提高BRDF的测量效率......
算法:
foreach outgoing direction wo
move light to illuminate surface with a thin beam from wo
for each incoming direction wi
move sensor to be at direction wi from surface
measure incident radiance
参考资料
完整笔记
- 度盘链接
- 提取码:njcf











 加油
加油


